Operaciones combinadas

 

¿Qué son las operaciones combinadas?

Son expresiones numéricas en las que pueden aparecer varias operaciones (sumas, restas, multiplicaciones o divisiones) con paréntesis, corchetes, llaves o sin más.

¿Cómo resolvemos las operaciones combinadas?

Para resolver las operaciones combinadas hay que seguir unos sencillos pasos:

1. Resolver primero la operación o las operaciones que haya dentro de los paréntesis.
2. Si hay varias operaciones seguidas, primero se hacen las multiplicaciones y divisiones y después las sumas y restas.

Ejemplos resueltos de operaciones combinadas

Vamos a ver tres ejemplos, empezando por lo más fácil.

Ejemplo 1: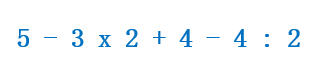

En este caso como no hay paréntesis tenemos que fijarnos en las operaciones: primero hacemos las multiplicaciones y divisiones que aparezcan:

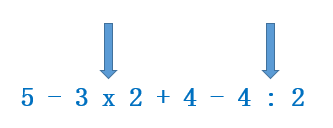
Una vez que las hemos identificado, debemos resolver las operaciones:

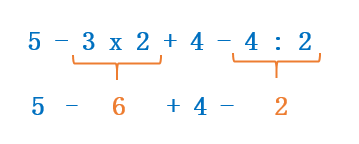
Ahora ya solo quedan sumas y restas, por lo tanto resolvemos la expresión:

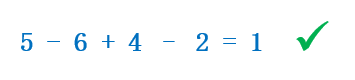
Ejemplo 2: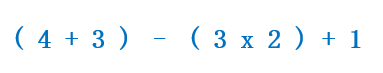

En este ejemplo, hay paréntesis por tanto, tenemos que resolver primero las operaciones que hay dentro de ellos:

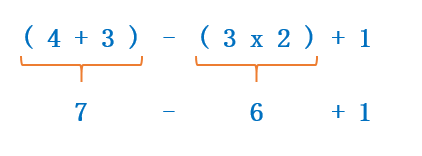
Ahora nos fijamos en las operaciones que quedan, pero solo son sumas y restas. Por tanto, podemos operar de izquierda a derecha y resolvemos la expresión: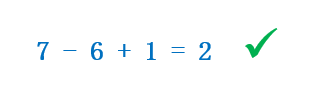

Ejemplo 3:

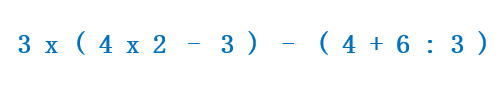
En este ejemplo, tenemos paréntesis. Por tanto, tenemos que resolver las operaciones que hay dentro de ellos. ¡Cuidado! Dentro de los paréntesis hay varias operaciones, por eso tenemos que fijarnos en hacer primero las multiplicaciones y divisiones dentro de los paréntesis: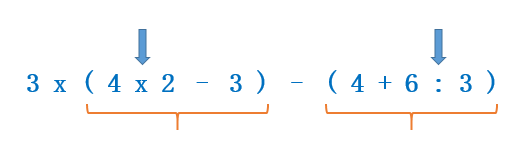

Una vez que tengamos presente qué operaciones son las que tenemos que resolver primero, podemos calcularlas:

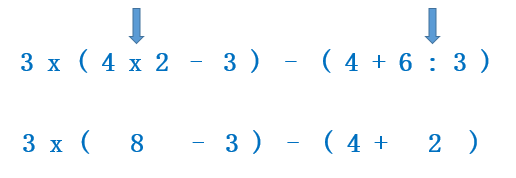
Ahora, como dentro de los paréntesis hay solo una operación podemos resolverlos:

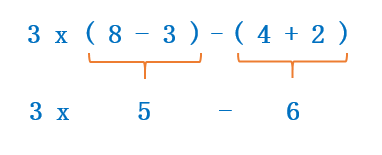
Una vez quitados los paréntesis volvemos a fijarnos en las operaciones. Primero hay que hacer la multiplicación:

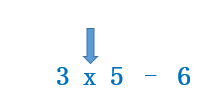
Una vez resuelta la multiplicación podemos resolver la expresión:

Ejercicio 1

 Realiza las siguientes operaciones teniendo en cuenta su prioridad:

 1 27 + 3 x 5 – 16 =

 2 27 + 3 – 45 : 5 + 16 =

 3 (2 x 4 + 12) x (6 − 4) =

 4 3 x 9 + (6 + 5 – 3) – 12 : 4 =

 5 2 + 5 x (2 x 3)³ =

 6 440 − [30 + 6 x (19 − 12)] =

 7 2 x {4 x [7 + 4 x (5 x 3 − 9)] − 3 x (40 − 8)} =

Resuelve aquí los ejercicios

Ejercicio 2

 Realiza las siguientes operaciones:

 1(3 − 8)+ [5 − (−2)] =

 2 5 − [6 − 2 − (1 − 8) − 3 + 6] + 5 =

 3 9 : [6 : (− 2)] =

 4 [(− 2)5 − (−3)³]² =

 5 (5 + 3 x 2 : 6 − 4 ) x (4 : 2 − 3 + 6) : (7 − 8 : 2 − 2)² =

 6 [(17 − 15)³ + (7 − 12)²] : [(6 − 7) x (12 − 23)] =

Resuelve aquí los ejercicios

 Fuente:

https://www.smartick.es/blog/matematicas/recursos-didacticos/operaciones-combinadas-con-ejemplos/

https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/racionales/ejercicios-resueltos-de-operaciones-combinadas.html

 

Unidades de volumen

 

Unidades de volumen

Llamamos volumen de un cuerpo al espacio que ocupa. Como tal espacio tiene 3 dimensiones: largo, ancho y alto.

Cada unidad de volumen es 1 000 veces mayor que la unidad inmediatamente inferior y 1 000 veces menor que la unidad inmediatamente superior.

La unidad de volumen es el metro cúbico (m³), que equivale a un cubo de 1 metro arista.

Por su relevancia y uso, las unidades que más vas a utilizar son el m³, el dm³ y el cm³.

El m³ es una unidad muy grande para medir el volumen que ocupan algunos objetos. Necesitamos otras medidas más pequeñas, son los submúltiplos.

Decímetro cúbico (dm³): Es el volumen ocupado por un cubo cuya arista mide 1 dm; equivale a 1 : 1000  = 0,001 m³.

Centímetro cúbico (cm³): Es el volumen ocupado por un cubo cuya arista mide 1 cm; equivale a 1 : 1 000 000  = 0,000 001 m³. Un dm³ contiene 10x10x10=1 000 cm³

¿Qué unidad de volumen utilizar en cada caso?

• El volumen que ocupa el agua de una piscina de 25 m de larga, 12 m de ancha y 2 m de profundidad es de 600 m³. No llega a 1 dam³.
• El embalse de Tanes tiene un volumen retenido de 33,27 hm³ en una superficie de 159 ha.
• Caudal medio anual del río Nalón: 11,67 m³/s.
• Caudal medio del río Amazonas: 230 000 m³/s.
• Volumen de los océanos: 1 300 000 000 km³.
• Garrafa de 5 litros de agua: 5 dm³.

1.- Copia y completa en tu cuaderno:

a) 5 m³ =…………..…..dm³;              7 dm³ = ………... mm³;         7526 cm3 = …………dm³

b) 560 dam³ =………… hm³;            15 km³ =…………hm³;          86 m³ =…………….. hm³

c) 0,56 m³ =…………… cm³;            23,56 dm³ = ……. m³;           0,6 dm³ =……….……cm³

Volumen, capacidad y masa: relaciones.

Existen relaciones muy útiles entre las unidades de volumen, capacidad y masa. Así, un litro es la capacidad de un cubo de un decímetro de arista, y un kilogramo es la masa de dicho cubo cuando está lleno de agua destilada.

Volumen y capacidad.

Se define el litro como el volumen de un cubo de un decímetro de arista, es decir, un decímetro cúbico. Esa es la equivalencia fundamental entre las unidades de volumen y de capacidad.

Un litro es la capacidad de un cubo de 1 dm de arista: 1 dm³ = 1 l.

La siguiente tabla muestra las equivalencias entre las unidades de volumen y capacidad.

Unidades de volumen	m3			dm3			cm3
Unidades de capacidad	kl	hl	dal	l	dl	cl	ml

Volumen, capacidad y masa.

Si un recipiente con agua destilada de 1 litro de capacidad (que ocupa 1 dm³) lo pesamos en una balanza,  esta se equilibraría exactamente con una pesa de 1 kg.

La siguiente tabla muestra las equivalencias entre las unidades de volumen, capacidad y masa para el agua destilada.

Hay líquidos más pesados que el agua destilada, como el mercurio, y más ligeros, como el aceite. Así un litro de mercurio pesa 13,6 kg, y un litro de aceite, 0,92 kg. Se debe a la densidad de los distintos elementos.

2.- Un depósito con un volumen de 0,5 m³ y 12 dm³ está lleno de agua. Para vaciar el depósito se abre el grifo que echa 3 dal y 2 l de agua por minuto. Calcula el tiempo en segundos que se emplea para vaciar el depósito. Pasa el resultado a forma compleja en horas, minutos y segundos.

3.- Calcula la cantidad de agua que puede contener un recipiente de forma cúbica que tiene 1,5 m de arista. Expresa el resultado en litros.

4.- Un camión cisterna transporta 66 hl de leche. Se envasa la mitad en recipientes de 1 dm³ y la otra mitad en botellas de 75 cl. ¿Cuántos recipientes de cada tipo se necesitan?

5.- De un grifo mal cerrado se desprende una gota de agua cada segundo. ¿Cuántos litros de agua se perderán si el grifo está goteando 15 días y 15 gotas de agua equivalen a 15 cm³.

6.- Una piscina rectangular de 15 m de largo, 6 m de ancho y 2 m de profundidad se pinta con una pintura impermeable a razón de 5,25 € el metro cuadrado. ¿Cuánto cuesta pintar toda la piscina?

7.- Se quiere losar el suelo de un patio rectangular de 20 m de largo y 7,5 m de ancho con losetas cuadradas de 50 cm de la­do. Si cada loseta cuesta 3,5 €, ¿cuál es el precio total de las losetas necesarias?

8.- Una finca se compone de un terreno rectangular de 200 me­tros de largo por 27,5 metros de ancho, y de un terreno cua­drado de 45 metros de lado. ¿Cuál es la superficie total de la finca en áreas?

9.- Completa en tu cuaderno:

548,2 m³ a litros:...............          45 m³ a kg........................           6 714 dm³ a m³..........................

431cl a dm3........................         0,45 t a dm3  ...................           875,7 ml a dm³...........................

45 kg a cm³.........................        0,15 m³ a q.......................           45,25 dm³ a ml...........................

10.- Queremos pintar una habitación que mide 10 m de larga, 6 m de ancha y 2,50 m de alta. La superficie ocupada por ventanas, puertas y otros espacios que no se pintan es de 12 m². Calcula el importe de la pintura que necesitamos si un bote de 4 kg cuesta 15 euros y da para pintar 32 m². Ten en cuenta que el suelo no lo pintamos, sí el techo.

11.- Si cada cubito es 1 cm³, ¿cuál es el volumen de cada una de estas figuras?

12.- Un depósito de agua puede almacenar hasta 13,31 m³. ¿Cuánto tiempo tardarían en llenarlo dos grifos que vierten, cada minuto, 9 y 13 litros, respectivamente? Expresa el resultado de forma compleja.

13.- Escoge la unidad en que medirías el volumen de los objetos de la izquierda. Utiliza m³, dm³ y cm³

Un bote de refresco
Una piscina
Un cubilete del parchís
Un paquete de leche	dm3
Una botella de zumo
Una casa de 8 pisos
Un teléfono móvil	cm3

Fuente: https://sites.google.com/a/baudilioarce.com/matematicas-6/10-sistema_de_medidas/10-6-unidades-de-volumen

 

Cuerpos de revolución

Espacios de nombres

Acciones de página

Cuerpos de revolución Concepto: Los cuerpos de revolución son los cuerpos geométricos que se forman al girar una figura plana alrededor de un eje.

Cuerpos de revolución. Cuando una figura plana gira alrededor de un eje se obtiene un cuerpo de revolución. Los tres cuerpos de revolución más importantes son el cilindro, el cono y la esfera.
La observación de la naturaleza nos muestra la existencia de variadas formas en los cuerpos materiales que la componen y nos proporciona la idea de volumen, superficie, línea, y punto.
Por necesidades prácticas, el desarrollo de técnicas usadas para medir, construir o desplazarse, llevaron al hombre a hacer uso de las diversas propiedades de las figuras geométricas y, en muchos casos a formar “cuerpos” a partir de estas.

Sumario

 [ocultar] 

• 1 Reseña histórica
• 2 Cilindro
  • 2.1 Definición y elementos
  • 2.2 Cálculo del área
  • 2.3 Cálculo del volumen
• 3 Cono
  • 3.1 Definición y elementos
  • 3.2 Área del cono
  • 3.3 Cálculo de su volumen
• 4 Esfera
  • 4.1 Definición y elementos
  • 4.2 Cálculo del área de una esfera
  • 4.3 Volumen de la esfera
• 5 Fuente

Reseña histórica

La Geometría es una de las más antiguas ciencias. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto, Estrabón y Diodoro Sículo.

Una vez adquiridas estas nociones y prescindiendo de su origen práctico, la Geometría (medición de la Tierra), de ser un conjunto de técnicas, pasó a constituir una disciplina matemática formal, donde la figura geométrica es un ente abstracto y sus propiedades el objeto de estudio de la Geometría.

Cilindro

Definición y elementos

El cilindro es el cuerpo que se obtiene a partir de un rectángulo que gira alrededor de uno de sus lados.

Cálculo del área

Si se desarrolla la superficie lateral del cilindro de radio r y de altura h, se obtiene una superficie plana que es un rectángulo.
El largo del rectángulo es igual a la longitud de las circunferencias que limitan las bases ( L= 2πr ) y su altura es igual a la altura del cilindro.

Por tanto el área lateral (AL) del cilindro es igual al área del rectángulo ABCD obtenido.

El área total (AT) del cilindro es igual a la suma del área lateral y las de sus dos bases.

Sustituyendo

Se obtiene:

Y es de esta forma que se puede hallar el área del cilindro.

Cálculo del volumen

El volumen de un prisma es igual al producto del área de la base por la altura:

Esta misma fórmula es la que se utiliza para calcular el volumen de un cilindro.

Cono

Definición y elementos

El cono es el cuerpo obtenido de un triángulo rectángulo que gira alrededor de uno de sus catetos.

Área del cono

Si se desarrolla la superficie lateral del cono de radio r, generatriz g y altura h, se obtiene una superficie plana que es un sector circular de radio g, determinado por un arco b cuya longitud es igual a la longitud de la circunferencia de la base: b = 2πr.

Por tanto:

El área lateral del cono es igual al área del sector circular así obtenido. El área del sector circular se calcula utilizando la proporción siguiente:

Sustituyendo en (1)

El área total del cono circular recto es igual a la suma del área lateral y el área de su base.

Cálculo de su volumen

La relación que existe entre los volúmenes de un prisma y el de una pirámide que tengan iguales las bases y la altura, es la misma que existe entre los volúmenes de un cilindro y un cono que cumplan estas mismas condiciones.

O sea: el volumen de un cono de radio r y altura h es igual a la tercera parte del volumen del cilindro de igual radio y altura.

Esfera

Definición y elementos

La esfera es el cuerpo que se obtiene a partir de un semicírculo que gira alrededor de su diámetro.

Cálculo del área de una esfera

El área de una esfera de radio r es el área de la superficie curva que la limita:

Volumen de la esfera

El volumen de una esfera de radio r es:

Se puede comprobar experimentalmente que el volumen de un cono de radio r y la altura h con h = 2r, es igual a la mitad del volumen de la esfera del mismo radio.

Fuente

• Libro de texto de Matemática, 8vo grado. Editorial Pueblo y Educación, 1990.
• https://www.ecured.cu/Cuerpos_de_revoluci%C3%B3n#:~:text=Los%20cuerpos%20de%20revoluci%C3%B3n%20son,el%20cono%20y%20la%20esfera. 

El mínimo común múltiplo

Una radio emisora emite cada 15 minutos una invitación para una fiesta;otra emisora emite la misma invitación cada 20 minutos. ¿Cada cuantos minutos coincidirán ambas emisoras en emitir la misma invitación?

Veamos la frecuencia de las invitaciones en ambas emisoras. para ello debemos calcular los múltiplos de 15 y 20.

1ra empresa = 15, 30, 45, 60, 75, 90, 105, 120, 135...

2da empresa =  24, 40, 60, 80, 100, 120, 140...

Los primeros múltiplos de 15 y 20, sin tomar en cuenta el 0, son 60, 120 y 180. De ellos, el mínimo es 60. Por lo tanto, decimos que el mínimo cómun múltiplo de 15 y 20 es 60 y se escribe asi: 

m.c.m. (15, 20) = 60

Ahora un vídeo